Sejarah Penemuan Gerbang Logika
Pada tahun 1854 George Boole menciptakan logika simbolik yang sekarang dikenal dengan aljabar Boole. Setiap peubah (variabel) dalam aljabar Boole hanya memiliki dua keadaan atau dua harga, yaitu "keadaan benar" yang dinyatakan dengan " 1 " atau "keadaan salah" yang dinyatakan dengan " 0 "
Kemudian aljabar Boole diwujudkan berupa sebuah piranti atau sistem yang disebut "Gerbang Logika".
Gerbang logika adalah piranti dua keadaan, yaitu mempunyai keluaran dua keadaan: keluaran dengan nol volt yang menyatakan logika 0 (atau rendah) dan keluaran dengan tegangan tetap yang menyatakan logika 1 (atau tinggi).
Gerbang logika dapat mempunyai beberapa masukan yang masing-masing mempunyai salah satu dari dua keadaan logika, yaitu 0 atau 1.
Gerbang-gerbang logika yang khususnya dipakai di dalam sistem digital, dibuat dalam bentuk IC (Integrated Circuit) yang terdiri atas transistor-transistor, diode dan komponen-komponen lainnya.
Jenis - jenis Gerbang Logika
Terdapat 7 jenis Gerbang Logika Dasar yang membentuk sebuah Sistem Elektronika Digital, yaitu :
- Gerbang AND
- Gerbang OR
- Gerbang NOT
- Gerbang NAND
- Gerbang NOR
- Gerbang X-OR (Exclusive OR)
- Gerbang X-NOR (Exlusive NOR)
Dari ke-7 jenis diatas, Gerbang Logika dibagi menjadi 2 :
1. Gerbang Logika Inverter (Pembalik), contohnya Gerbang Logika NOT (NOT Gate)
2. Gerbang Logika Non-Inverter, contohnya Gerbang Logika AND,OR,NAND,NOR,XO,XNOR
Gerbang AND (AND Gate)
Gerbang AND memerlukan 2 atau lebih Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang AND akan menghasilkan Keluaran (Output) Logika 1 jika semua masukan (Input) bernilai Logika 1 dan akan menghasilkan Keluaran (Output) Logika 0 jika salah satu dari masukan (Input) bernilai Logika 0. Simbol yang menandakan Operasi Gerbang Logika AND adalah tanda titik (“.”) atau tidak memakai tanda sama sekali. Contohnya : Z = X.Y atau Z = XY.
Simbol dan Tabel Kebenaran Gerbang AND (AND Gate)
Diagram Waktu Gerbang AND
Gerbang OR (OR Gate)
Gerbang OR memerlukan 2 atau lebih Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang OR akan menghasilkan Keluaran (Output) 1 jika salah satu dari Masukan (Input) bernilai Logika 1 dan jika ingin menghasilkan Keluaran (Output) Logika 0, maka semua Masukan (Input) harus bernilai Logika 0.
Simbol yang menandakan Operasi Logika OR adalah tanda Plus (“+”). Contohnya : Z = X + Y.
Simbol dan Tabel Kebenaran Gerbang OR (OR Gate)
Diagram Waktu Gerbang OR
Gerbang NOT (NOT Gate)
Gerbang NOT hanya memerlukan sebuah Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang NOT disebut juga dengan Inverter (Pembalik) karena menghasilkan Keluaran (Output) yang berlawanan (kebalikan) dengan Masukan atau Inputnya. Berarti jika kita ingin mendapatkan Keluaran (Output) dengan nilai Logika 0 maka Input atau Masukannya harus bernilai Logika 1. Gerbang NOT biasanya dilambangkan dengan simbol minus (“-“) di atas Variabel Inputnya.
Simbol dan Tabel Kebenaran Gerbang NOT (NOT Gate) 
Diagram Waktu Gerbang NOT
Gerbang NAND (NAND Gate)
Arti NAND adalah NOT AND atau BUKAN AND, Gerbang NAND merupakan kombinasi dari Gerbang AND dan Gerbang NOT yang menghasilkan kebalikan dari Keluaran (Output) Gerbang AND. Gerbang NAND akan menghasilkan Keluaran Logika 0 apabila semua Masukan (Input) pada Logika 1 dan jika terdapat sebuah Input yang bernilai Logika 0 maka akan menghasilkan Keluaran (Output) Logika 1.
Simbol dan Tabel Kebenaran Gerbang NAND (NAND Gate) 
Diagram Waktu Gerbang NAND
Gerbang NOR (NOR Gate)
Arti NOR adalah NOT OR atau BUKAN OR, Gerbang NOR merupakan kombinasi dari Gerbang OR dan Gerbang NOT yang menghasilkan kebalikan dari Keluaran (Output) Gerbang OR. Gerbang NOR akan menghasilkan Keluaran Logika 0 jika salah satu dari Masukan (Input) bernilai Logika 1 dan jika ingin mendapatkan Keluaran Logika 1, maka semua Masukan (Input) harus bernilai Logika 0.
Simbol dan Tabel Kebenaran Gerbang NOR (NOR Gate) 
Diagram Waktu Gerbang NOR
Gerbang X-OR (X-OR Gate)
X-OR adalah singkatan dari Exclusive OR yang terdiri dari 2 Masukan (Input) dan 1 Keluaran (Output) Logika. Gerbang X-OR akan menghasilkan Keluaran (Output) Logika 1 jika semua Masukan-masukannya (Input) mempunyai nilai Logika yang berbeda. Jika nilai Logika Inputnya sama, maka akan memberikan hasil Keluaran Logika 0.
Simbol dan Tabel Kebenaran Gerbang X-OR (X-OR Gate) 
Diagram Waktu Gerbang X-OR
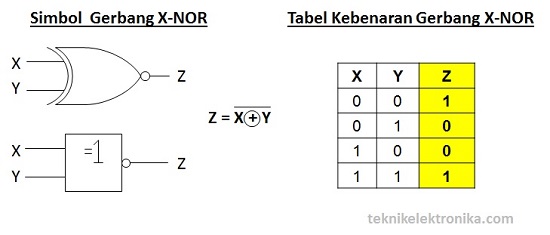
Gerbang X-NOR (X-NOR Gate)
Seperti Gerbang X-OR, Gerban X-NOR juga terdiri dari 2 Masukan (Input) dan 1 Keluaran (Output). X-NOR adalah singkatan dari Exclusive NOR dan merupakan kombinasi dari Gerbang X-OR dan Gerbang NOT. Gerbang X-NOR akan menghasilkan Keluaran (Output) Logika 1 jika semua Masukan atau Inputnya bernilai Logika yang sama dan akan menghasilkan Keluaran (Output) Logika 0 jika semua Masukan atau Inputnya bernilai Logika yang berbeda. Hal ini merupakan kebalikan dari Gerbang X-OR (Exclusive OR).
Simbol dan Tabel Kebenaran Gerbang X-NOR (X-NOR Gate) 
Aljabar Boolean
Aljabar boolean, adalah sistem aljabar himpunan atau proposisi yang memenuhi aturan-aturan ekivalen logis.
- Misalkan B dengan operasi + (OR) dan * (AND), atau suatu komplemen, dan dua elemen yang beda 0 dan 1 yang didefinisikan pada himpunan atau proposisi, sehingga a,b dan c merupakan elemen B yang mempunyai sifat-sifat identitas, komutatif, distributif dan komplemen.
- Misalkan F dengan operasi + (OR) dan ● (AND), atau suatu komplemen (‘), dan dua elemen yang beda 0 dan 1 yang didefinisikan pada himpunan atau proposisi, sehingga a,b dan c merupakan elemen B yang mempunyai sifat-sifat identitas, komutatif, distributif dan komplemen.
Fungsi Aljabar Boolean :
Terdapat 2 jenis Teorema dalam Aljabar Boolean :
– Teorema variabel tunggal :
Teorema variable tunggal diperoleh dari hasil penurunan operasi logika dasar OR, AND, dan NOT yang mana teorema itu meliputi teorema 0 dan 1, identitas idempotent, komplemen dan involusi.
– Teorema variabel jamak :
Teorema variable jamak terdiri dari teorema komutatif, distributive, asosiatif, absorsi dan morgan.
Hukum Aljabar Boolean
Dengan menggunakan Hukum Aljabar Boolean ini, kita dapat mengurangi dan menyederhanakan Ekspresi Boolean yang kompleks sehingga dapat mengurangi jumlah Gerbang Logika yang diperlukan dalam sebuah rangkaian Digital Elektronika.
Berikut 6 tipe Hukum yang berkaitan dengan Hukum Aljabar Boolean :1. Hukum Komutatif (Commutative Law)
Hukum Komutatif menyatakan bahwa penukaran urutan variabel atau sinyal Input tidak akan berpengaruh terhadap Output Rangkaian Logika.
Contoh :
Perkalian (Gerbang Logika AND)
X.Y = Y.X
Penjumlahan (Gerbang Logika OR)
X+Y = Y+X
X+Y = Y+X
Catatan : Pada penjumlahan dan perkalian, kita dapat menukarkan posisi variabel atau dalam hal ini adalah sinyal Input, hasilnya akan tetap sama atau tidak akan mengubah keluarannya.
2. Hukum Asosiatif (Associative Law)
Contoh :
Hukum Asosiatif menyatakan bahwa urutan operasi logika tidak akan berpengaruh terhadap Output Rangkaian Logika.
Contoh :
Perkalian (Gerbang Logika AND)
W . (X . Y) = (W . X) . Y
Penjumlahan (Gerbang Logika OR)
W + (X + Y) = (W + X) + Y
W + (X + Y) = (W + X) + Y
Catatan : Pada penjumlahan dan perkalian, kita dapat mengelompokan posisi variabel dalam hal ini adalah urutan operasi logikanya, hasilnya akan tetap sama atau tidak akan mengubah keluarannya. Tidak peduli yang mana dihitung terlebih dahulu, hasilnya tetap akan sama. Tanda kurung hanya sekedar untuk mempermudah mengingat yang mana akan dihitung terlebih dahulu.
Hukum Distributif menyatakan bahwa variabel-variabel atau sinyal Input dapat disebarkan tempatnya atau diubah urutan sinyalnya, perubahan tersebut tidak akan mempengaruhi Output Keluarannya.
4. Hukum AND (AND Law)
Disebut dengan Hukum AND karena pada hukum ini menggunakan Operasi Logika AND atau perkalian. Berikut ini contohnya :
5. Hukum OR (OR Law)
Hukum OR menggunakn Operasi Logika OR atau Penjumlahan. Berikut ini adalah Contohnya :
6. Hukum Inversi (Inversion Law)
Hukum Inversi menggunakan Operasi Logika NOT. Hukum Inversi ini menyatakan jika terjadi Inversi ganda (kebalikan 2 kali) maka hasilnya akan kembali ke nilai aslinya.
Jadi, jika suatu Input (masukan) diinversi (dibalik) maka hasilnya akan berlawanan. Namun jika diinversi sekali lagi, hasilnya akan kembali ke semula.
Referensi:
- https://teknikelektronika.com/pengertian-gerbang-logika-dasar-simbol/
- 6.-Elektronika-Digital-Gerbang-logika-Aljabar-Boolean.pdf
No comments:
Post a Comment